10684. Улучшение дорог

В стране есть n городов и n – 1 двусторонняя дорога, причем из любого города можно добраться до любого другого, двигаясь только по дорогам. Города пронумерованы целыми числами от 1 до n включительно.

Все дороги изначально считаются плохими, однако правительство планирует улучшить состояние некоторых из них. Граждане будут довольны улучшением, если на пути от столицы, расположенной в городе 1, до любого другого города будет не более одной плохой дороги.

Определите количество способов улучшить качество некоторых дорог, чтобы удовлетворить это требование. Так как ответ может быть очень большим, выведите его по модулю 10⁹ + 7.

Вход. В первой строке задано одно целое число n (2 ≤ n ≤ 2 * 10⁵) – количество городов в стране. Во второй строке задано n – 1 целых положительных чисел p₂, p₃, p₄, ..., p_n (1 ≤ p_i ≤ i – 1) – описание дорог страны. Число p_i означает, что в стране имеется дорога, соединяющая город p_i и город i.

Выход. Выведите количество способов улучшить качество дорог по модулю 10⁹ + 7.

Пример входа 1	Пример выхода 1
3 1 1	4
Пример входа 2	Пример выхода 2
6 1 2 2 1 5	15

РЕШЕНИЕ

дерево

Анализ алгоритма

Пусть f(v) – количество способов улучшить качество дорог для поддерева с корнем в вершине v. Обозначим через to сына вершины v.

· Если дорога (v, to) остается плохой, то все дороги в поддереве с корнем в вершине to должны быть улучшены.

· Если дорогу (v, to) улучшить, то количество способов улучшить качество дорог для поддерева с корнем в вершине to равно f(to).

Пусть to₁, to₂, …, to_k – сыновья v. Тогда

f(v) = (f(to₁) + 1) * (f(to₂) + 1) * … * (f(to_k) + 1)

Если v – лист (вершина, не имеющая сыновей), то положим f(v) = 1.

Пример

Рассмотрим примеры, приведённые в условии. Для каждой вершины v запишем значение f(v).

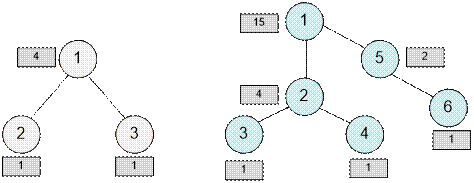
В первом примере существует 4 способа улучшить качество дорог, при которых на пути от города 1 до любого другого города имеется не более одной плохой дороги. Плохие дороги обозначены пунктирными линиями, а хорошие –сплошными.

Реализация алгоритма

Все вычисления выполняются по модулю MOD = 10⁹ + 7.

#define MOD 1000000007

Функция dfs вычисляет значение f(v) – количество способов улучшить качество дорог для поддерева с корнем в вершине v. Предком v является вершина p.

long long dfs(int v, int p = -1)

{

long long s = 1;

Если to₁, to₂, …, to_k – сыновья v, то

f(v) = (f(to₁) + 1) * (f(to₂) + 1) * … * (f(to_k) + 1)

for (int to : g[v])

if (to != p)

{

long long sub = dfs(to, v);

s = (s * (sub + 1)) % MOD;

}

return s;

}

Читаем входные данные. Строим дерево.

scanf("%d", &n);

g.resize(n + 1);

for (i = 2; i <= n; i++)

{

scanf("%d", &p);

g[i].push_back(p);

g[p].push_back(i);

}

Вычисляем и выводим результат.

res = dfs(1);

printf("%lld\n", res);